What we aim ?

GeomScale is a research and development project that delivers open source code for state-of-the-art algorithms at the intersection of data science, optimization, geometric, and statistical computing.

The current focus of GeomScale is scalable algorithms for sampling from high-dimensional distributions, integration, convex optimization, and their applications. One of our ambitions is to fill the gap between theory and practice by turning state-of-the-art theoretical tools in geometry and optimization to state-of-the-art implementations.

We believe that towards this goal, we will deliver various innovative solutions in a variety of application fields, like finance, computational biology, and statistics that will extend the limits of contemporary computational tools.

GeomScale aims in serving as a building block for an international, interdisciplinary, and open community in high dimensional geometrical and statistical computing.

Financial crisis prediction computed with volesti package using a public dataset that covers 10 years, from January 2006 to December 2016, and comprises a set of 52 popular exchange traded funds (ETFs) and the US central bank (FED) rate of return. The graph shows financial crisis, warning periods and normal periods.

Scientific background, problems and applications

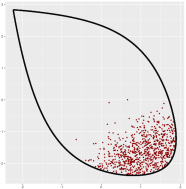The main computational problem we study is sampling from high-dimensional distributions. Sampling is a fundamental operation that plays a crucial role across sciences including modern machine learning and data science. To address this problem we develop and implement Markov Chain Monte Carlo sampling methods that scale up to thousands of dimensions. We also work on the development of practical algorithms based on sampling for a set of fundamental computational problems such as convex optimization, integration, volume computation and Bayesian inference.

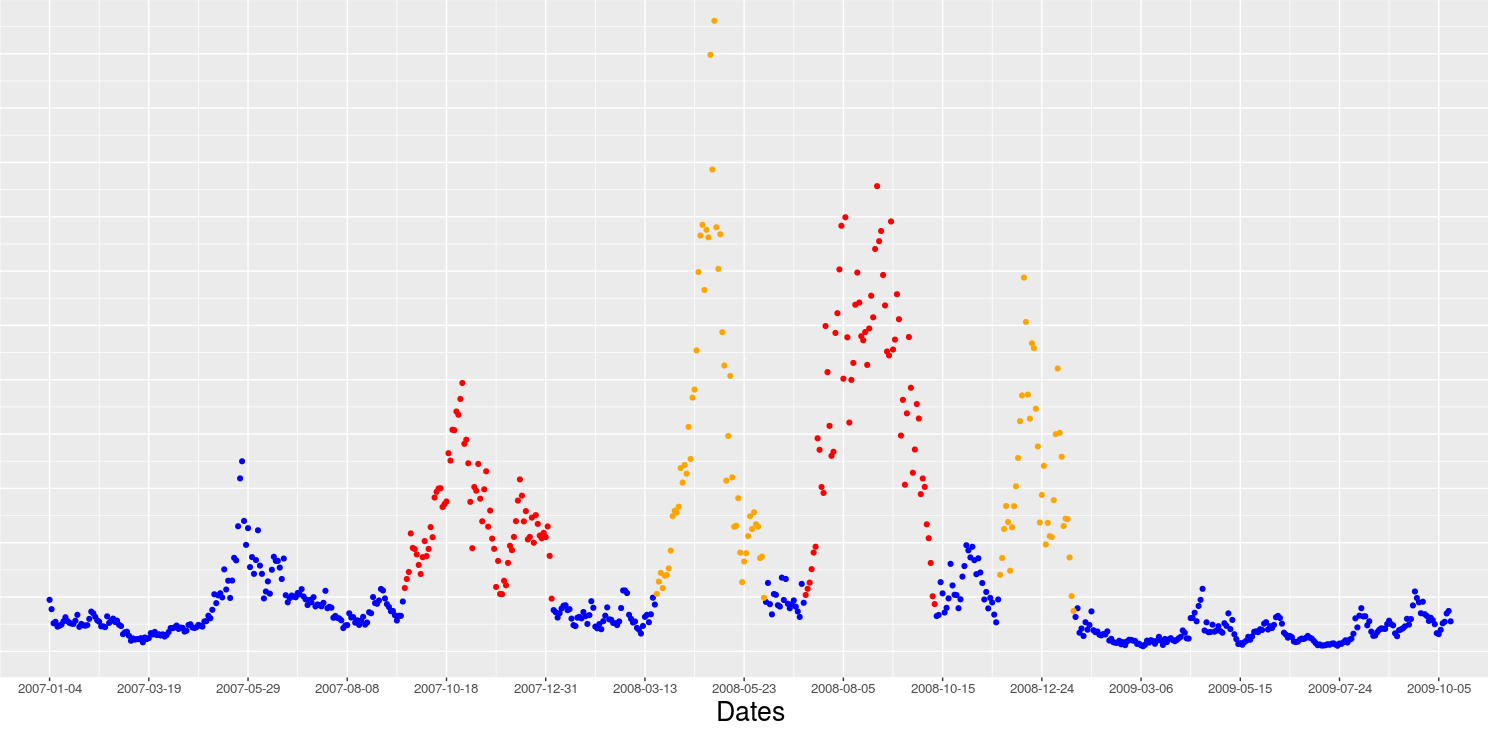
Regarding applications, GeomScale provides efficient geometric modeling and algorithms that are useful in computational finance, in particular in financial crisis and anomaly detection, portfolio scoring and portfolio optimization. Moreover, GeomScale hosts a software framework for analysis of metabolic networks that given a metabolic model generates high-dimensional random sampling of metabolic fluxes that in turn provide an unbiased description of the capabilities of the metabolic network.